Dimensions of Physical Quantities

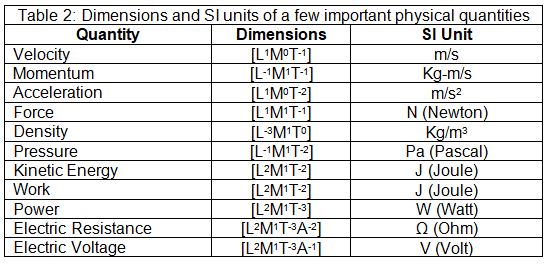
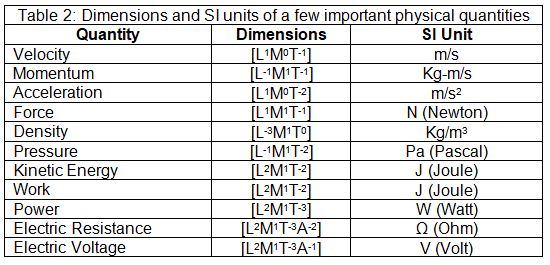
As we know, physical quantities can be categorized in fundamental and derived quantities (see here). The seven fundamental quantities form the seven dimensions for the physical quantities. The dimensions of the fundamental quantities are given in table 1. Dimensions of the derived quantities can be written in terms of fundamental quantities. The power to which the base quantities are raised to represent a physical quantity is known as the dimensions of that quantity. The dimensions are denoted by the square bracket [ ]. Table 2 shows the dimensions of a few important quantities.

Table 1: Dimensions of fundamental quantities
Fundamental Quantity	Dimension
Length	[L]
Mass	[M]
Time	[T]
Current	[A]
Temperature	[K]
Amount of substance	[mol]
Luminous Intensity	[cd]

Important points regarding dimensions of physical quantities:

• Principle of homogeneity of dimensions: Only the quantities with the same dimensions can be added or subtracted.
• Dimensional consistency: Both sides of a mathematical equation must have the same dimensions.
• Dimensional consistency is necessary, but not sufficient, condition for a valid equation.
• If the dependence of a physical quantity on other quantities is known, the relationship among physical quantities can be deduced with the help of dimensional analysis. Limitations:
• Dimensionless constants cannot be obtained
• Physical quantities with the same dimensions are indistinguishable